ECUACUINES
Una ecuación es una igualdad matemática entre dos expresiones algebraicas, denominadas miembros, en las que aparecen valores conocidos odatos, y desconocidos o incógnitas, relacionados mediante operaciones matemáticas. Los valores conocidos pueden ser números, coeficientes oconstantes; y también variables cuya magnitud pueda ser establecida a través de las restantes ecuaciones de un sistema, o bien mediante otros procesos. Las incógnitas, representadas generalmente por letras, constituyen los valores que se pretende hallar. Por ejemplo, en la ecuación:
la variable  representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. La igualdad planteada por una ecuación será cierta o falsa dependiendo de los valores numéricos que tomen las incógnitas; se puede afirmar entonces que una ecuación es una igualdad condicional, en la que sólo ciertos valores de las variables (incógnitas) la hacen cierta.
representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. La igualdad planteada por una ecuación será cierta o falsa dependiendo de los valores numéricos que tomen las incógnitas; se puede afirmar entonces que una ecuación es una igualdad condicional, en la que sólo ciertos valores de las variables (incógnitas) la hacen cierta.
 representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. La igualdad planteada por una ecuación será cierta o falsa dependiendo de los valores numéricos que tomen las incógnitas; se puede afirmar entonces que una ecuación es una igualdad condicional, en la que sólo ciertos valores de las variables (incógnitas) la hacen cierta.
representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. La igualdad planteada por una ecuación será cierta o falsa dependiendo de los valores numéricos que tomen las incógnitas; se puede afirmar entonces que una ecuación es una igualdad condicional, en la que sólo ciertos valores de las variables (incógnitas) la hacen cierta.
Se llama solución de una ecuación a cualquier valor individual de dichas variables que la satisfaga. Para el caso dado, la solución es:
Resolver una ecuación es encontrar su dominio solución, que es el conjunto de valores de las incógnitas para los cuales la igualdad se cumple. Por lo general, los problemas matemáticospueden expresarse en forma de una o más ecuaciones;[cita requerida] sin embargo no todas las ecuaciones tienen solución, ya que es posible que no exista ningún valor de la incógnita que haga cierta una igualdad dada. En ese caso, el conjunto de soluciones de la ecuación será vacío y se dice que la ecuación no es resoluble. De igual modo, puede tener un único valor, o varios, o incluso infinitos valores, siendo cada uno de ellos una solución particular de la ecuación. Si cualquier valor de la incógnita hace cumplir la igualdad (esto es, no existe ningún valor para el cual no se cumpla) la ecuación es en realidad una identidad.
INTRODUCCION
De manera más general, una ecuación tendrá la forma
donde F, G son operadores y a, b pueden ser valores numéricos, variables o funciones (en este último caso se tiene una ecuación funcional). Por ejemplo, la ecuación real (donde las incógnitas están sobre los números reales):
tiene por soluciones o raíces para:
el conjunto valores:
y para:
las raíces:
Siendo i un número entero.
Podemos ver:
con las soluciones:
Para i un número entero.
Uso de ecuaciones
La ciencia utiliza ecuaciones para enunciar de forma precisa leyes; estas ecuaciones expresan relaciones entre variables. Así, en física, la ecuación de la dinámica de Newton relaciona las variables fuerza F, aceleración a y masa m: F = ma. Los valores que son solución de la ecuación anterior cumplen la primera ley de la mecánica de Newton. Por ejemplo, si se considera una masa m = 1 kg y una aceleración a = 1 m/s, la única solución de la ecuación es F = 1 Kg·m/s = 1 Newton, que es el único valor para la fuerza permitida por la ley.
El campo de aplicación de las ecuaciones es inmenso, y por ello hay una gran cantidad de investigadores dedicados a su estudio.
Tipos de ecuaciones
Las ecuaciones pueden clasificarse según el tipo de operaciones necesarias para definirlas y según el conjunto de números sobre el que se busca la solución. Entre los tipos más frecuentes están:
- Ecuaciones algebraicas
- Polinómicas o polinomiales
- De primer grado o lineales
- De segundo grado o cuadráticas
- Racionales, aquellas en las que uno o ambos miembros se expresan como un cociente de polinimios
- Ecuaciones trascendentes, cuando involucran funciones no polinómicas, como las trigonométricas, exponenciales, etc.
- Diofánticas o diofantinas
- Ecuaciones diferenciales
- Ecuaciones integrales


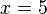
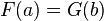
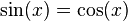







No hay comentarios:
Publicar un comentario