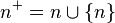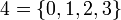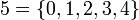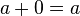NUMEROS NATURALES
Un número natural es cualquiera de los números que se usan para contar los elementos de un conjunto.
CONSTRUCCIONES ACCIOMATICAS
Históricamente, se han realizado propuestas para axiomatizar la noción habitual de números naturales, de entre las que destacan las de Peano y la construcción a partir de la teoría de conjuntos.
Axiomas de Peano
Los axiomas de Peano rigen la estructura de los números naturales sin necesidad de otra teoría (por ejemplo, la de conjuntos) ni de las nociones aritméticas de suma o equivalencia. Requiere, eso sí, de la noción previa de sucesor. Los cinco axiomas de Peano son (definición sin el cero):
- El 1 es un número natural.
- Si n es un número natural, entonces el sucesor de n también es un número natural.
- El 1 no es el sucesor de ningún número natural.
- Si hay dos números naturales n y m con el mismo sucesor, entonces n y m son el mismo número natural.
- Si el 1 pertenece a un conjunto de números A, y además siempre se verifica que: dado un número natural cualquiera que esté en A, su sucesor también pertenece a A; entonces Acontiene al conjunto de todos los números naturales. Este es el axioma de inducción, que captura la idea de inducción matemática.
Definición en teoría de conjuntos
En teoría de conjuntos se define al conjunto de los números naturales como el mínimo conjunto que es inductivo. La idea es que se pueda contar haciendo una biyección desde un número natural hasta el conjunto de objetos que se quiere contar. Es decir, para dar la definición de número 2, se requiere dar un ejemplo de un conjunto que contenga precisamente dos elementos. Esta definición fue proporcionada por Bertrand Russell, y más tarde simplificada por Von Neumann quien propuso que el candidato para 2 fuera el conjunto que contiene solo a 1 y a 0.
Formalmente, un conjunto  se dice que es un número natural si cumple
se dice que es un número natural si cumple
 se dice que es un número natural si cumple
se dice que es un número natural si cumple- Para cada
 ,
, 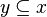
- La relación
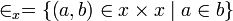 es un orden total estricto en
es un orden total estricto en 
- Todo subconjunto no vacío de
 tiene elementos mínimo y máximo en el orden
tiene elementos mínimo y máximo en el orden 
Se intenta pues, definir un conjunto de números naturales donde cada elemento respete las convenciones anteriores. Primero se busca un conjunto que sea el representante del 0, lo cual es fácil ya que sabemos que  no contiene elementos. Luego se definen los siguientes elementos de una manera ingeniosa con el uso del concepto de sucesor.
no contiene elementos. Luego se definen los siguientes elementos de una manera ingeniosa con el uso del concepto de sucesor.
 no contiene elementos. Luego se definen los siguientes elementos de una manera ingeniosa con el uso del concepto de sucesor.
no contiene elementos. Luego se definen los siguientes elementos de una manera ingeniosa con el uso del concepto de sucesor.
Se define-según Halmos- entonces que el conjunto vacío es un número natural que se denota por  y que cada número natural
y que cada número natural  tiene un sucesor denotado como
tiene un sucesor denotado como 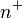 . Estas ideas quedan formalizadas mediante las siguientes expresiones:
. Estas ideas quedan formalizadas mediante las siguientes expresiones:
 y que cada número natural
y que cada número natural  tiene un sucesor denotado como
tiene un sucesor denotado como 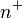 . Estas ideas quedan formalizadas mediante las siguientes expresiones:
. Estas ideas quedan formalizadas mediante las siguientes expresiones:
De esta manera, cada elemento de algún número natural es un número natural; a saber, un antecesor de él. Por ejemplo:
- Por definición
 (lo cual refuerza el hecho de que 0 no tiene antecesores)
(lo cual refuerza el hecho de que 0 no tiene antecesores) - 1 es el sucesor de 0, entonces

- 2 es el sucesor de 1, pero 1 es {0}, entonces
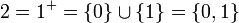
- y en general
Esto permite establecer una relación de orden entre los elementos del conjunto a pesar de que un conjunto es por naturaleza un agregado de elementos desordenados. Se define esta relación mediante la expresión
También se puede usar otra definición más inmediata a partir del hecho de que cada número natural consta de sus antecesores. Así  si y sólo si
si y sólo si  .
.
 si y sólo si
si y sólo si  .
.
Ésa es la construcción formal de los naturales que garantiza su existencia como conjunto a la luz del desarrollo axiomático Zermelo-Fraenkel. El postulado de los conjuntos infinitos asegura la validez de la técnica de demostración conocida como inducción matemática.
Un teorema demuestra que cualquier conjunto que sea inductivo contiene a todos los números naturales, es decir que si  es un conjunto inductivo, entonces
es un conjunto inductivo, entonces  . Esto significa que, en efecto,
. Esto significa que, en efecto,  es el mínimo conjunto inductivo.
es el mínimo conjunto inductivo.
 es un conjunto inductivo, entonces
es un conjunto inductivo, entonces  . Esto significa que, en efecto,
. Esto significa que, en efecto,  es el mínimo conjunto inductivo.
es el mínimo conjunto inductivo.
Lo que convierte a los números naturales  en un monoide conmutativo con elemento neutro 0, el llamado Monoide Libre con un generador. Este monoide satisface la propiedadcancelativa y por lo tanto puede incluirse en un grupo matemático. El menor grupo que contiene a los naturales es el de los números enteros.
en un monoide conmutativo con elemento neutro 0, el llamado Monoide Libre con un generador. Este monoide satisface la propiedadcancelativa y por lo tanto puede incluirse en un grupo matemático. El menor grupo que contiene a los naturales es el de los números enteros.
 en un monoide conmutativo con elemento neutro 0, el llamado Monoide Libre con un generador. Este monoide satisface la propiedadcancelativa y por lo tanto puede incluirse en un grupo matemático. El menor grupo que contiene a los naturales es el de los números enteros.
en un monoide conmutativo con elemento neutro 0, el llamado Monoide Libre con un generador. Este monoide satisface la propiedadcancelativa y por lo tanto puede incluirse en un grupo matemático. El menor grupo que contiene a los naturales es el de los números enteros.
Esto convierte  (esto es, ℕ con esta nueva operación), en un monoide conmutativo.
(esto es, ℕ con esta nueva operación), en un monoide conmutativo.
 (esto es, ℕ con esta nueva operación), en un monoide conmutativo.
(esto es, ℕ con esta nueva operación), en un monoide conmutativo.
Otra forma de construcción de  es la siguiente: Sea
es la siguiente: Sea 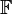 la clase de todos los conjuntos y definiremos una relación binaria R "ser equipotente" de la siguiente manera Dados A y B∈
la clase de todos los conjuntos y definiremos una relación binaria R "ser equipotente" de la siguiente manera Dados A y B∈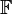 se dice que A R B
se dice que A R B  Existe una aplicación biyectiva de A sobre B,es decir,existe
Existe una aplicación biyectiva de A sobre B,es decir,existe  biyectiva. Claramente se puede demostrar que esta relación verifica las propiedades reflexiva,simétrica y transitiva luego es una relación de equivalencia al conjunto cociente
biyectiva. Claramente se puede demostrar que esta relación verifica las propiedades reflexiva,simétrica y transitiva luego es una relación de equivalencia al conjunto cociente ![\mathbb{F}/R\ = \{ [A] / A\in \mathbb{F} \}](http://upload.wikimedia.org/math/5/9/d/59d0f955deac98282b5cbf050f121c86.png) los llamaremos cardinales y a los cardinales finitos se les llamará números naturales.Las operaciones de suma y producto de cardinales se definen como el cardinal de la unión y el producto cartesiano de los conjuntos representantes y verifica todas las propiedades para que
los llamaremos cardinales y a los cardinales finitos se les llamará números naturales.Las operaciones de suma y producto de cardinales se definen como el cardinal de la unión y el producto cartesiano de los conjuntos representantes y verifica todas las propiedades para que  sea un semianillo conmutativo y unitario.
sea un semianillo conmutativo y unitario.
 es la siguiente: Sea
es la siguiente: Sea 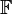 la clase de todos los conjuntos y definiremos una relación binaria R "ser equipotente" de la siguiente manera Dados A y B∈
la clase de todos los conjuntos y definiremos una relación binaria R "ser equipotente" de la siguiente manera Dados A y B∈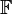 se dice que A R B
se dice que A R B  Existe una aplicación biyectiva de A sobre B,es decir,existe
Existe una aplicación biyectiva de A sobre B,es decir,existe  biyectiva. Claramente se puede demostrar que esta relación verifica las propiedades reflexiva,simétrica y transitiva luego es una relación de equivalencia al conjunto cociente
biyectiva. Claramente se puede demostrar que esta relación verifica las propiedades reflexiva,simétrica y transitiva luego es una relación de equivalencia al conjunto cociente ![\mathbb{F}/R\ = \{ [A] / A\in \mathbb{F} \}](http://upload.wikimedia.org/math/5/9/d/59d0f955deac98282b5cbf050f121c86.png) los llamaremos cardinales y a los cardinales finitos se les llamará números naturales.Las operaciones de suma y producto de cardinales se definen como el cardinal de la unión y el producto cartesiano de los conjuntos representantes y verifica todas las propiedades para que
los llamaremos cardinales y a los cardinales finitos se les llamará números naturales.Las operaciones de suma y producto de cardinales se definen como el cardinal de la unión y el producto cartesiano de los conjuntos representantes y verifica todas las propiedades para que  sea un semianillo conmutativo y unitario.
sea un semianillo conmutativo y unitario.